de fractalalbums
In de albums vind je naast afbeeldingen van gewone fractals ook, wat je zou kunnen noemen, 3D fractals. Feitelijk zijn ook dit gewone (2D) plaatjes, maar dan van fractals die in een 3D ruimte zijn bewerkt of gemanipuleerd.
Alle afbeeldingen in de album zijn eigen werk, gemaakt met verschillende computerprogramma's en de meeste zijn bewerkt in Photoshop. De links naar een aantal gebruikte programma's vind je op info en links
Hiernaast de fractal in zijn oer-vorm.

Mandelbrot en Julia
Benoit Mandelbrot is degene die in de jaren 80 van de vorige eeuw grotendeels verantwoordelijk was voor de grote vlucht die fractals hebben genomen. Hij liet de formule, zoals hiernaast in zijn eigen handschrift, met behulp van de computer berekenen en zo ontstond het bekende plaatje van de fractal (zie hierboven). Deze formule, ontdekt door de wiskundige Gaston Julia, is een wiskundige beschrijving van een fractal en herbergt een schat aan achterliggende mogelijkheden, zowel theoretisch, als grafisch, maar ook praktisch.
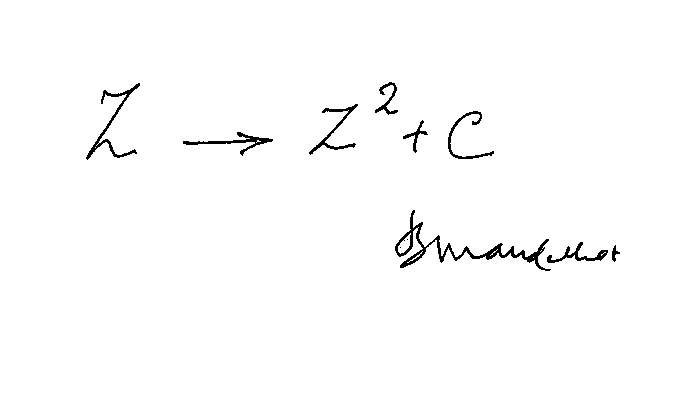
een beetje wiskunde
De kleur van elke pixel van elke fractal is het resultaat van een serie berekeningen, op basis van een of meer wiskundige formules. En daarmee zijn afbeeldingen van fractals vrijwel altijd een vorm van computer art.
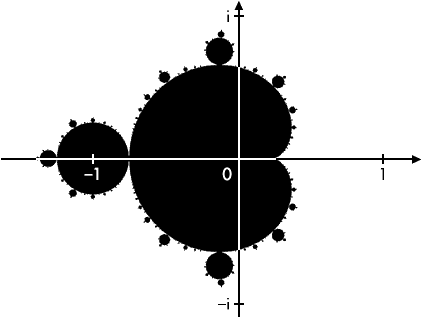
In grote lijnen, kun je zeggen, bestaan fractals uit patronen die zich op alle niveaus herhalen, maar de achterliggende wiskunde is (letterlijk) complex. De afbeelding hiernaast laat zien dat de fractal afgebeeld of geplot kan worden op een assenstelsel.
contact

